This post is a submission for a CU Boulder course colloquially known as DMU++, or Decision Making Under Uncertainty++.

Motivation and Questions

LLM-based planning seems to be quite the rage. From cobbled together star-farming Github repos, to a flood of research papers, to major initiatives by AI tech giants, there's a flood of demand for LLMs to be brought into the realm of planning.

There are two broad classes of LLM planners. LLM-as-a-planners attempt to utilize an LLM directly as a policy; given current state, have the LLM "reason" over the best action directly. A parallel method to this is LLM-as-a-modeler. With this approach, the LLM "reasons" over the problem domain, producing something like code for a heuristic policy or generating an MDP of the problem that can be solved independently of the LLM.

While reading through some papers on LLM-based planning, I was irked by how irrational many of the experiment setups are. Where some are just bad ideas, others are seemingly encumbered by ridiculous prompt hacking demonstrating a laziness to write a simple sanitizer. There seems to be a growing consensus that getting an LLM to reason successfully involves substantial hand-holding and detailed, guided examples of "how" it should reason. I reject this as completely insane. Look at some of the prompts of the papers I linked; could you, a human, read the prompt and give an answer in the desired format? Perhaps these authors intend to overcomplicate elementary problems, like stacking blocks, as an attempt to generalize to actually difficult problems.

So, I set out to make an equally contrived problem to better understand LLM-based planning and answer a few burning questions:

• Does an LLM perform better as-a-planner or as-a-modeler?
• Are short, simple, human-readable prompts effective?
• Do the "shall I be smarter?" reasoning knobs on an LLM actually work?

To limit the scope of this post, only the first and third question are really answered. The results allow for an opinion on the second question, but no comparative analysis is performed to establish a firmer answer. To limit the length of this post, I'll gloss over some of the implementation details and save them for a separate rant post.

Problem Overview

The scenario we'll be looking at is a simple block stacking problem. Functionally equivalent to one of those stack-the-rings-by-size puzzles for toddlers, where the LLM is asked to take a set of numbered blocks randomly placed into three stacks and sort them on the third stack.

Note that all images in this post can be clicked to enlarge.

Problem Space

The state space is represented by a straightforward list of lists, e.g. [[1, 0], [3], [4, 2]]. There are N!(N+1)(N+2)/2 possible states for N blocks (proof omitted), which comes in at 2520 states for 5 blocks.

The action space is for the "robot arm" to simply move the top block from one stack to another stack, so 6 permutations of Stack X to Stack Y. When an action is invalid, i.e. the source stack is empty, nothing happens to the state.

Experiment Setup

To analyze the performance of each approach, 50 random scenarios with 5 blocks each were generated. (While it would be interesting to look at performance with a larger number of blocks, we'll see that won't be necessary with today's LLMs.) Data on the success rate, the number of steps needed to solve each scenario, the number of OpenAI tokens used, and the wall time are collected. Across each tested policy, a limit of 20 steps is placed on each scenario. In the event of policy failure, such as the LLM generating nonsense, results in a default action to move from stack 1 to stack 2, which cannot incidentally let it reach the goal state.

For the LLM configuration, I used gpt-5-mini across all experiments, using the new agents SDK to create tools for the agent to invoke. The "reasoning level" setting is also configured from the choices of minimal, low, medium, and high. Apart from the tools and reasoning level, default settings are used.

Baseline Results

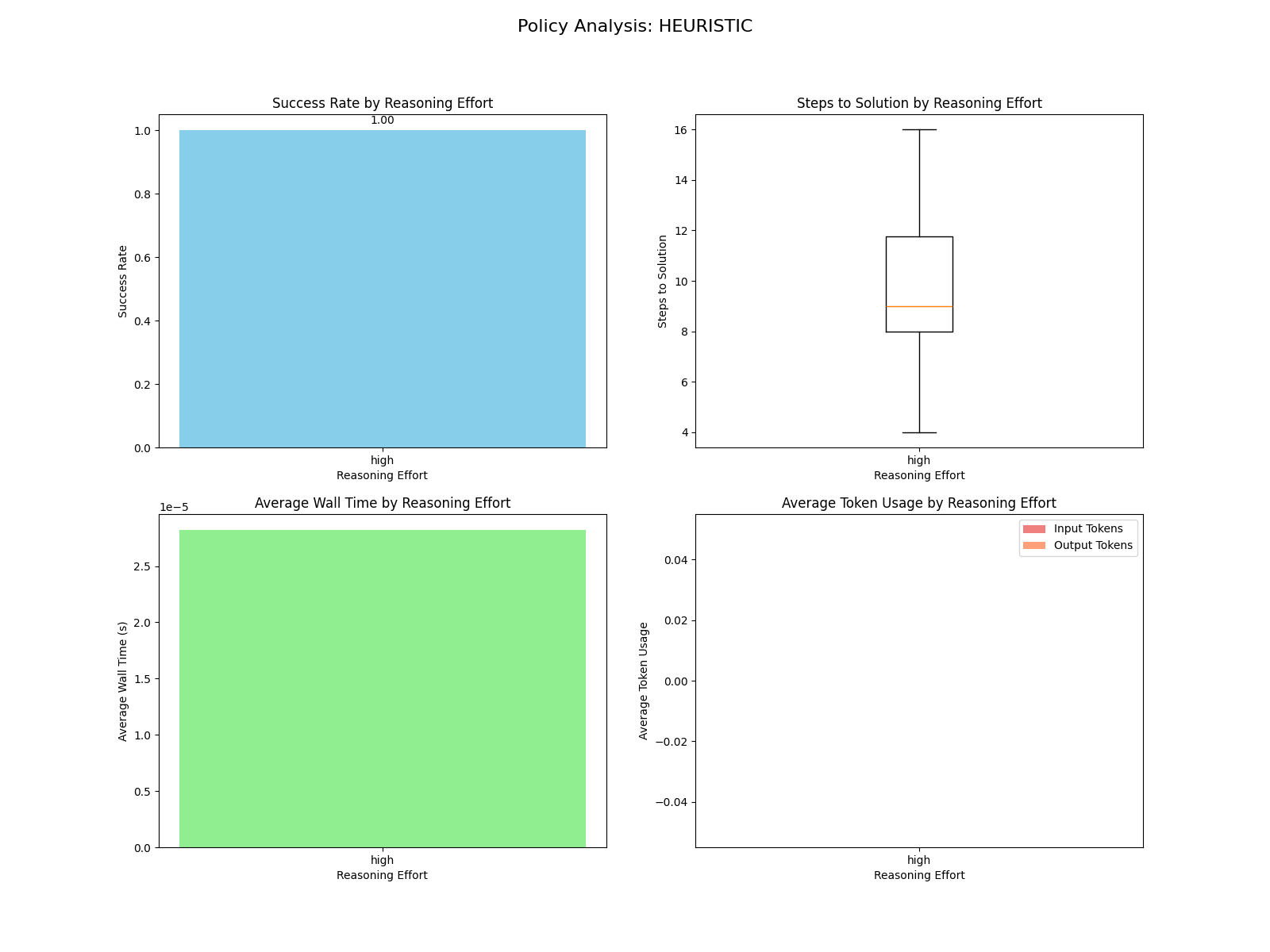
Heuristic

To compare against, I made a simple, 3 minutes of effort heuristic policy to compare against. It's certainly suboptimal and just greedily tries to get the next block onto stack 3. Here's some pseudocode:

def heuristic(state: State) -> Action:
  """Greedily stack the next block"""
  # Check if the goal stack is already sorted
  goal_sorted: bool = ...

  if not goal_sorted:
      # Move the blocks form the goal to the first stack
      return Action.MOVE_3_TO_1

  # Find the next block to move to the goal stack
  next_block: int = ...
  src_stack: int = ...
  block_on_top: bool = ...

  if block_on_top:
      return Action((src_stack, 3))

  # Move the top block to the other non-goal stack
  dst_stack = 3 - src_stack
  return Action((src_stack, dst_stack))

The plot is structured for the LLM planners, but we can observe that the heuristic always succeeds, takes up to 16 steps on a more difficult initial arrangement, and takes a couple dozen microseconds to run.

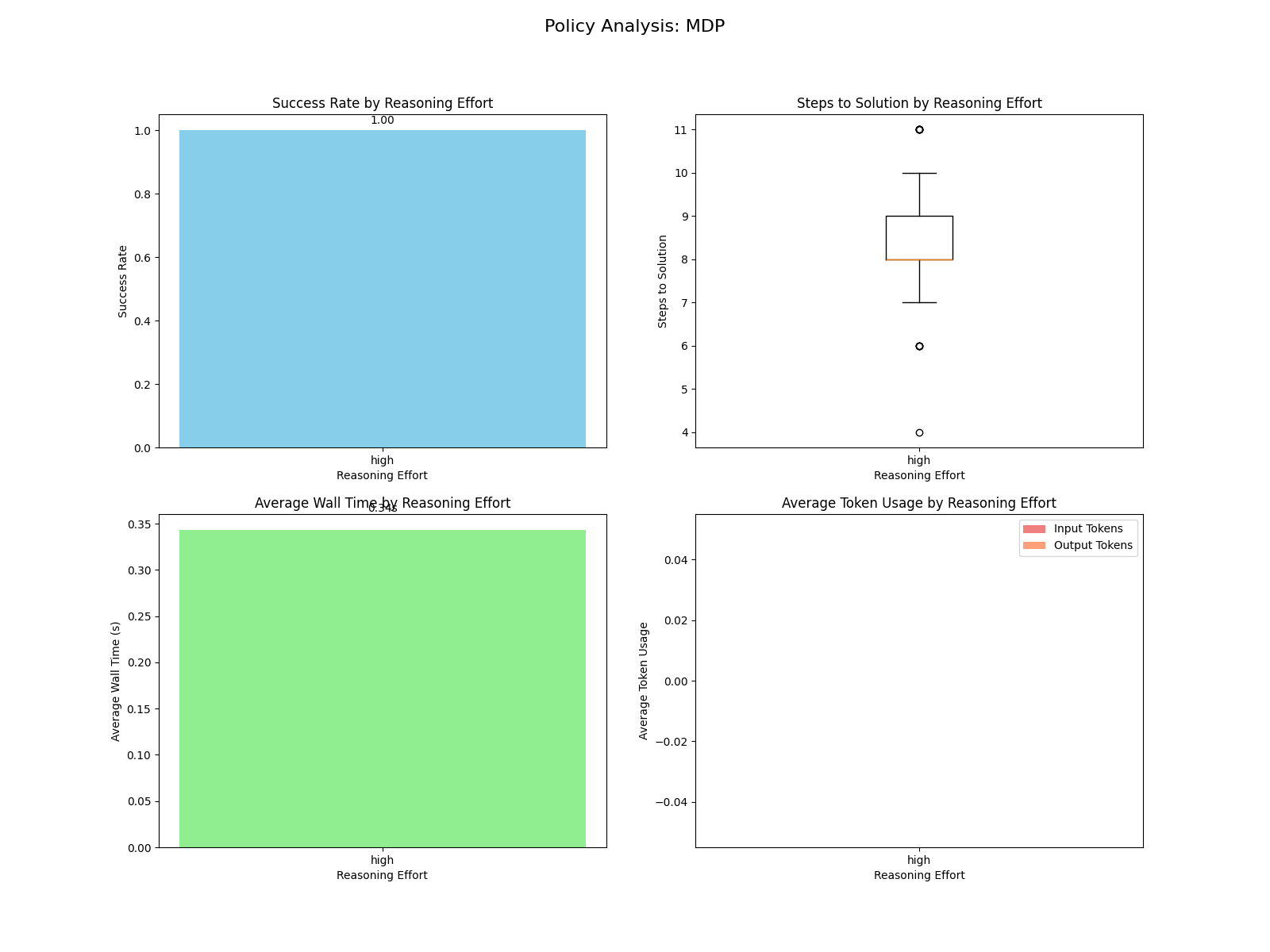
MDP

As an additional comparison, I model a Markov Decision Process for the problem. I spent more time than I care to admit implementing state_index to directly hash the state to a unique index; we'll discuss later how the LLM approaches this. The interface looks something like this (relevant for the MDP-LLM section):

class MDP:
  def __init__(self, num_blocks: int): ...

  def states(self) -> Generator[environment.State, None, None]:
      """Enumerate all possible states of the environment."""

  def state_index(self, state: environment.State) -> int: ...

  def actions(self) -> Generator[environment.Action, None, None]:
      """Enumerate all possible actions in the environment."""

  def action_index(self, action: environment.Action) -> int: ...

  def reward(self, state: environment.State, action: environment.Action) -> float: ...

  def transition(
      self, state: environment.State, action: environment.Action
  ) -> list[tuple[environment.State, float]]:
      """Transition a state-action pair into (next_state, probability) pairs."""

  def gamma(self) -> float: ...

Note that transition is deterministic in this simple scenario. Using a simple vectored value iteration, an optimal policy was created. Since the randomized scenarios require varying numbers of steps, we can see the optimal step count box-and-whisker plot takes an arbitrary shape. For the wall time, the time to compute the offline policy is plotted (online is a direct state-hash-to-action).

LLM-as-a-Planner Results

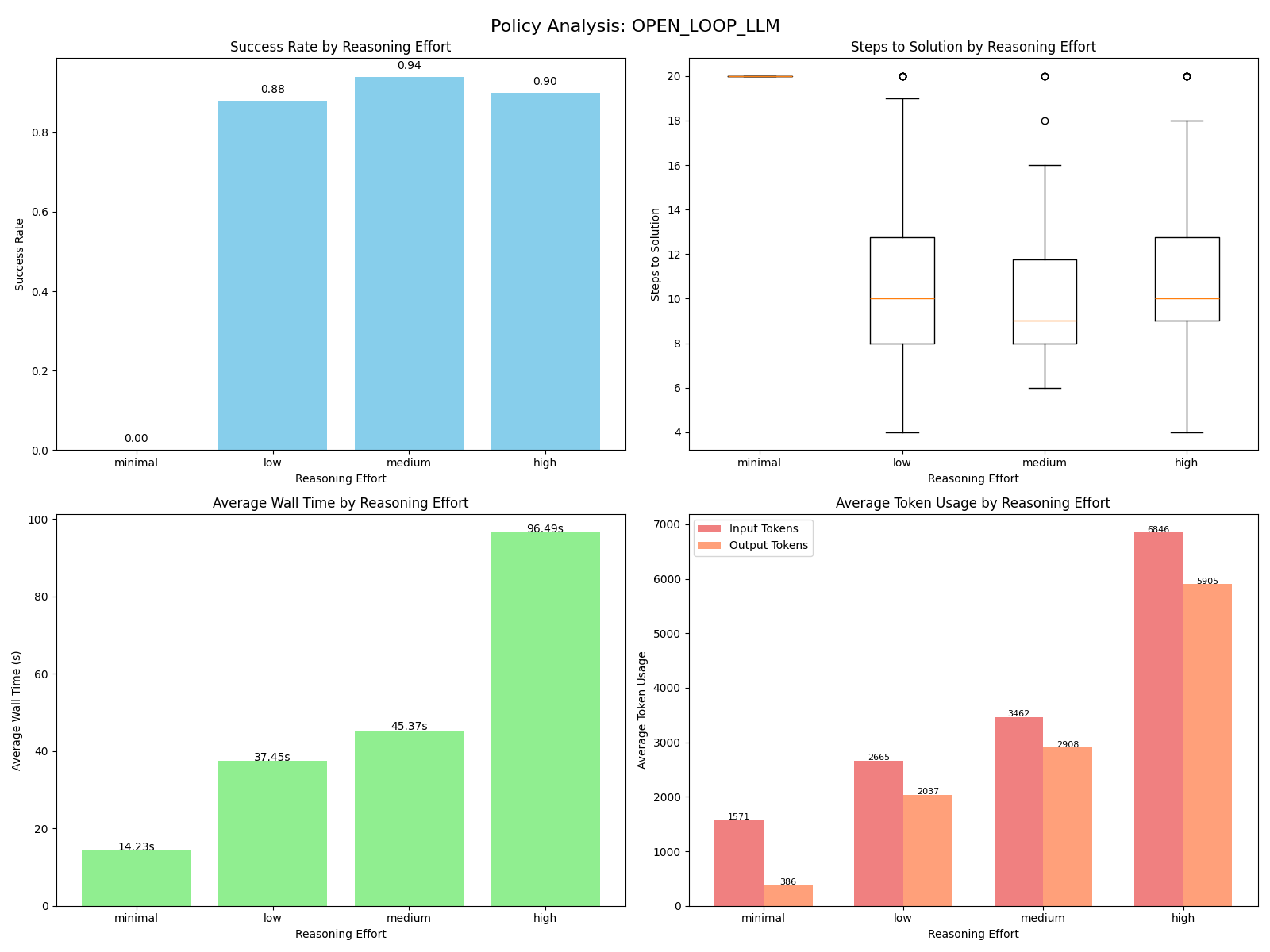
Open Loop LLM

Our first LLM-based policy is the simplest one: feed the LLM the current state of the environment and let it omnisciently produce a list of actions to bring the environment to the goal state. Since I'm focusing on simple prompts, I'll provide this one its entirety. All of the other polices have prompts that are close derivatives of this.

You are a robotic arm in a block world environment.

Your goal is to sort the blocks in ascending order on the third stack (Stack 3).
Each action involves moving the top block from one stack to another.
Use the provided tool to create a plan of actions to achieve this goal.

An example system state would be:
Stack 1: [2, 0]
Stack 2: [1]
Stack 3: [3, 4]

Where the goal state is:
Stack 1: []
Stack 2: []
Stack 3: [0, 1, 2, 3, 4]

When fed the tool, the LLM sees a simple create_plan(plan: list[Action]) -> None function it can call, as well as details on what the Action enum looks like. In case its plan falls short, I prompt it again to create a new plan, up to the 20 step limit.

This result shows our first surprises. The minimal reasoning is completely inept and always fails. Tuning the reasoning knob, the medium reasoning level actually performs the best in both success rate and the number of steps, but it fails to optimally solve the 4 step scenario. Perhaps the high reasoning setting makes the LLM overthink, as it has meaningfully worse performance. We can see our token usage ticks upwards with each reasoning level, with the high reasoning setting costing a little more than $0.01 per scenario. Of course, our overall planning time is just north of the microseconds our baseline policies need online. Just north.

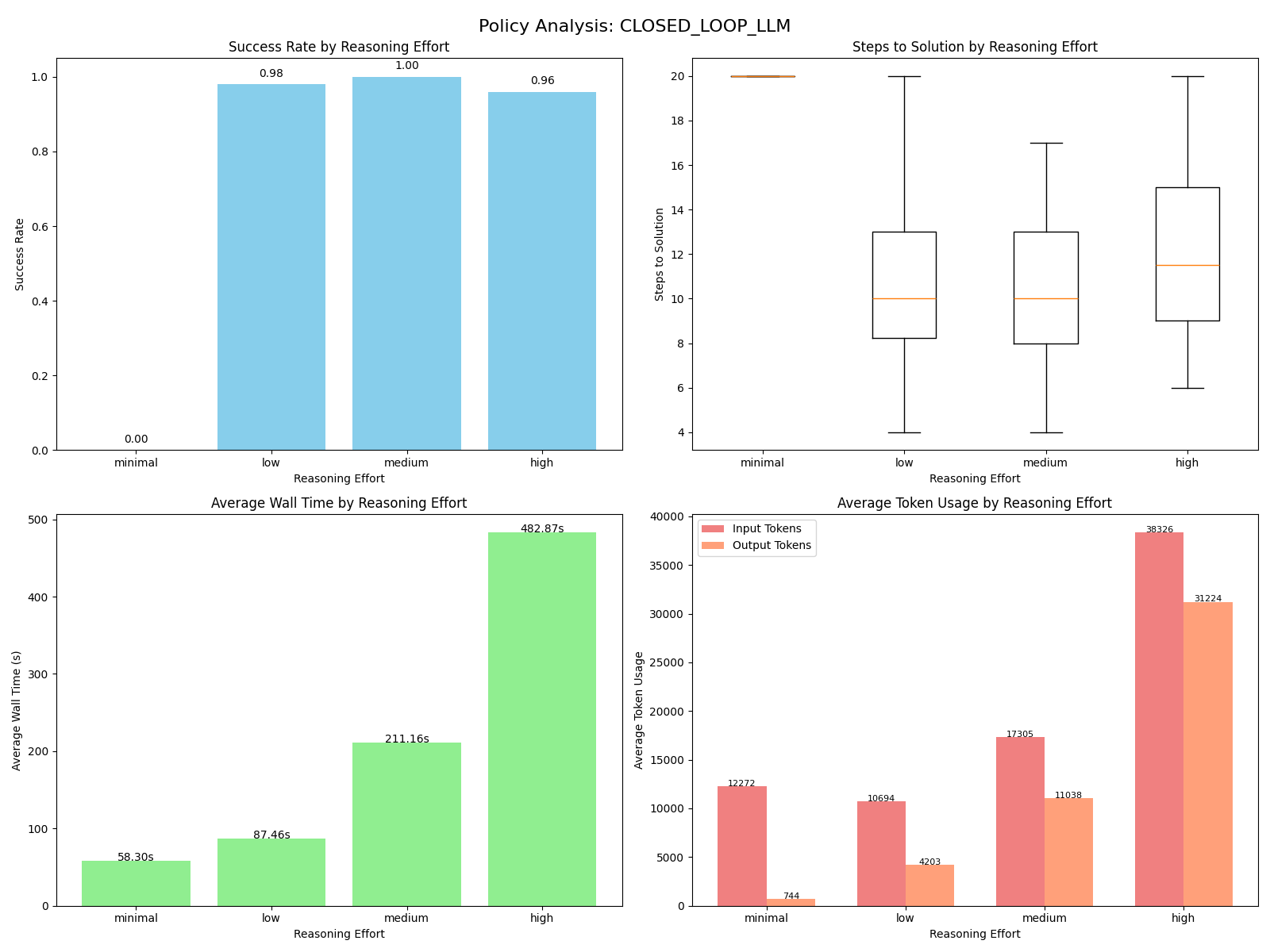
Closed Loop LLM

Our other LLM-as-a-planner policy is to use a "closed" loop, where we invoke the LLM to generate the single next action based on the current state. I did not bother setting up conversation context or any other means of letting the LLM think about its past mistakes, so "closed" is debatable.

Similar trends emerged in the closed loop results as the open loop planner, most notably that the best results occurred for the medium reasoning level. In contrast to the open loop planner, the closed loop takes even longer to run, costs about $0.07 per scenario at the high reasoning level, and generally takes more steps to reach the goal state. However, it also has higher success rates, with the medium reasoning closed loop planner being the only LLM-based planner that passes all 50 scenarios.

LLM-as-a-Modeler Results

For modeling results, we'll adjust our analysis a bit. Since the LLM only needs to be prompted once to create a heuristic function or write an MDP, we'll instead prompt it 50 times and run each solution against all 50 generated scenarios. Likewise to the MDP baseline, we'll plot the wall time as the offline computation time (including value iteration convergence for MDP-LLM). For both methods, the LLM gets one attempt to write the code and any failures to produce correct code, such as an import error or a runtime exception, results in a failure for that scenario or the entire batch, depending on where the error occurred.

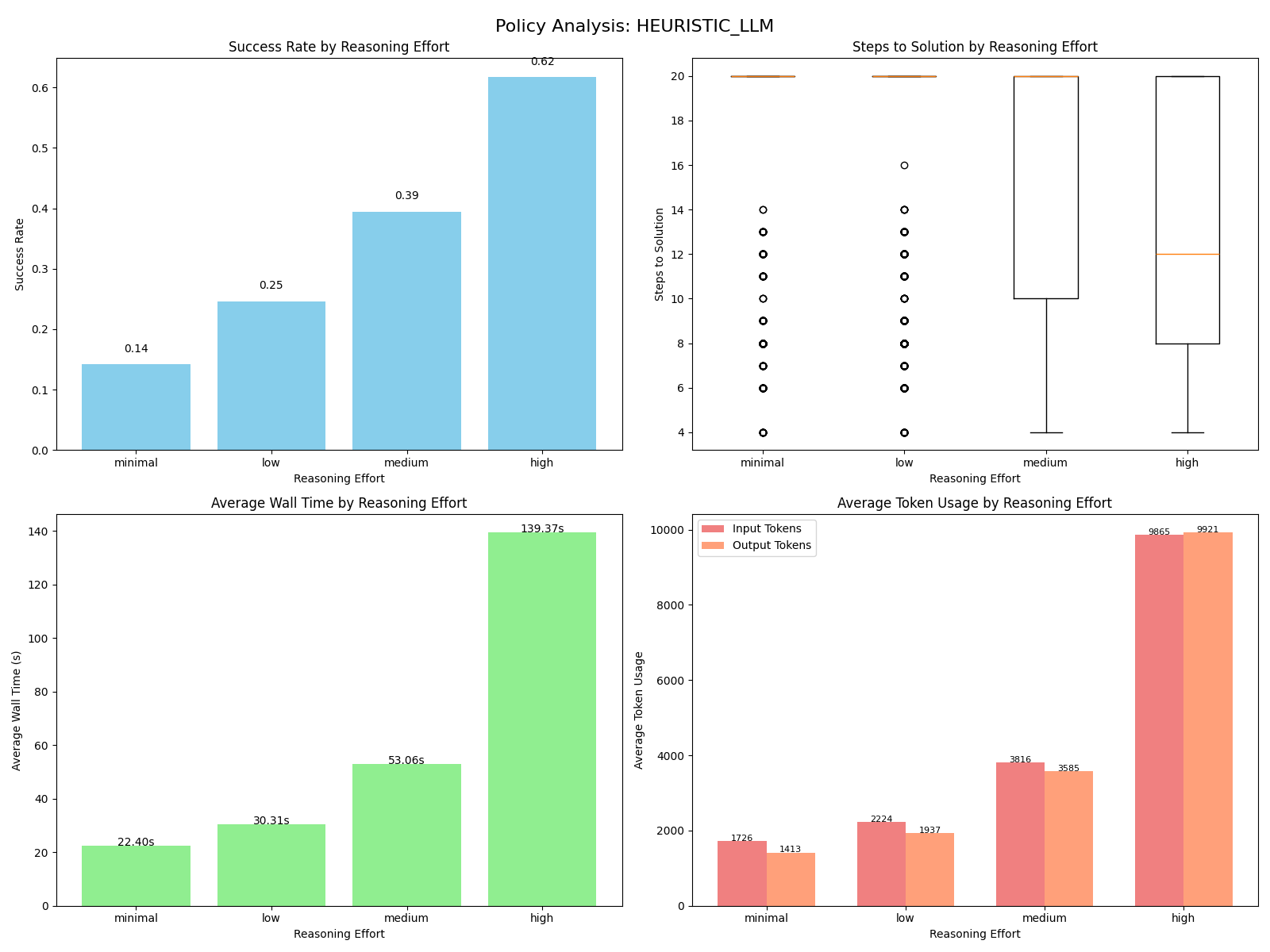
Heuristic LLM

The heuristic LLM works by prompting the LLM to write code that implements a simple policy function def heuristic(state: State) -> Action, running some modest checks on the output, then dynamically loading it into the simulator. In modification of the simple prompt given to the open loop LLM, the LLM is told to write a Python module and given some helper functions it may import.

The performance of this method was shockingly bad. Every reasoning level had some amount of success, but the high reasoning level failed to succeed more than two thirds of the time while burning quite a few tokens. Looking through the generated code, it's hard to pinpoint any particular error. The code reads much like a first year college student attempting to pass an autograder, but pretty consistently the LLM will lay out a coherent strategy in a docstring that doesn't quite match the code. Here's an example from the low reasoning level:

"""
Strategy:
  - Let next_needed = number of blocks already on stack 3 (they should be 0..next_needed-1).
  - If the top of any stack equals next_needed, move that block to stack 3.
  - Otherwise move the top block from the stack with the smallest top value to the other non-3 stack
    that either is empty or has a larger top (to avoid burying smaller blocks). If both choices
    are acceptable pick deterministically.
"""

That's a good idea! More complicated than the heuristic policy I implemented, but trying to avoid burying smaller blocks should allow for a better performing solution. Yet, come run time, the policy got stuck and hit the 20 step limit on every scenario.

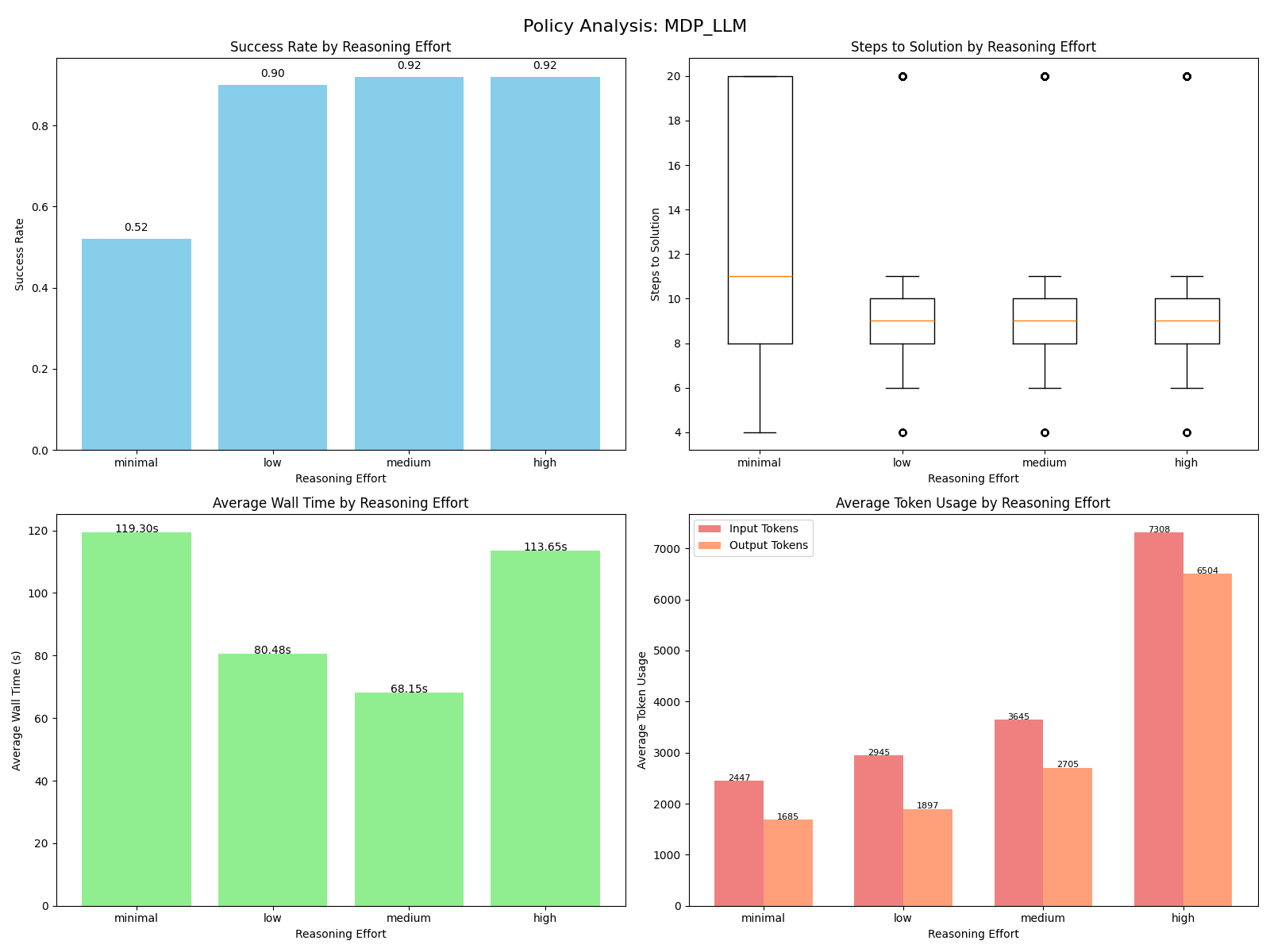
MDP LLM

Lastly, we have MDP LLM, where the LLM is given a similar prompt but instead asked to implement the interface shown in the baseline MDP section. The prompt also directed that vectored value iteration would be used on the MDP, so the state and action index functions needed to be handled with care (instructions I would give to a human writing this for me). No prompting was given to inform the LLM that the actions were deterministic, but every solution I checked correctly made this assumption anyways. In addition to the code checks, a 10 minute time limit was placed on the value iteration convergence to avoid solving for the halting problem on unboundedly bad implementations.

Remarkably, the LLM had a comparatively strong performance across all reasoning levels. Since a good implementation will converge to the optimal solution and a bad implementation will time out or raise an exception, the success rate corresponds to how often an optimal policy was found. While more samples would be needed to draw stronger conclusions, the tie in performance between the medium and high reasoning levels suggests a return of the pattern where the LLM "overthinks" the problem.

Looking through some of the generated MDPs, I was surprised to see the same pattern in nearly every solution and reasoning level. The difficult part in writing out the MDP is correctly enumerating all possible states and mapping them with a suitable state index. Nearly every solution looked like this:

    def __init__(self, num_blocks: int):
      self._state_cache = enumerate_states(num_blocks)
      self._index_cache = {simple_hash_function(state): i for i, state in enumerate(self._state_cache)}

  def states(self) -> Generator[environment.State, None, None]:
      for state in self._state_cache:
        yield state

  def state_index(self, state: environment.State) -> int:
      return self._index_cache[simple_hash_function(state)]

This is much simpler than figuring out how to directly hash to a sequential index, so I was delightfully surprised to see nearly every solution use this simpler solution without direct guidance. Most failures happened with either poorly converged policies or hitting the 10 minute timeout, suggesting that minor code deficiencies either failed to uniquely index a given state or degraded the performance of state enumeration too much.

Bringing it All Together

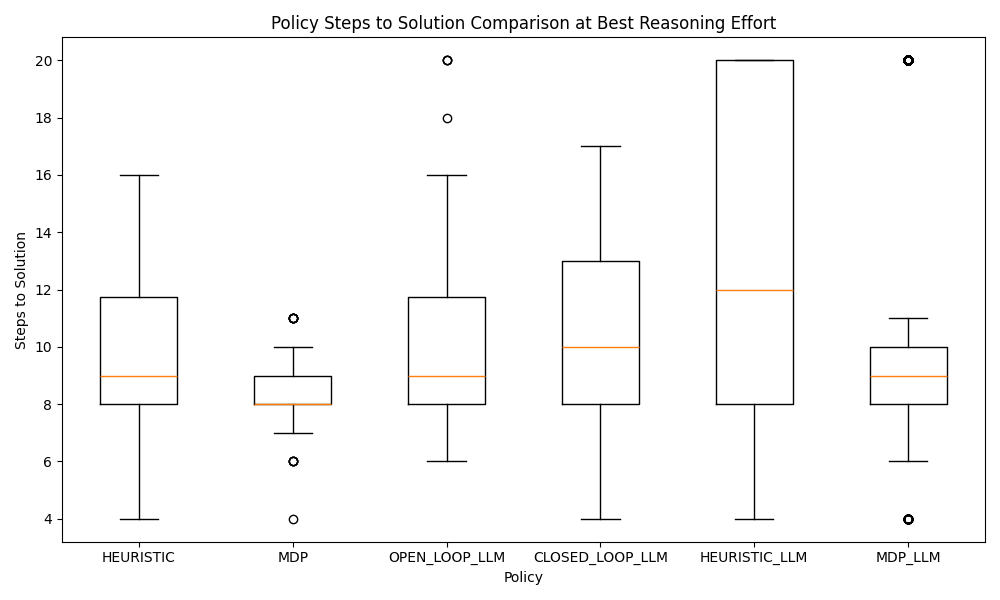
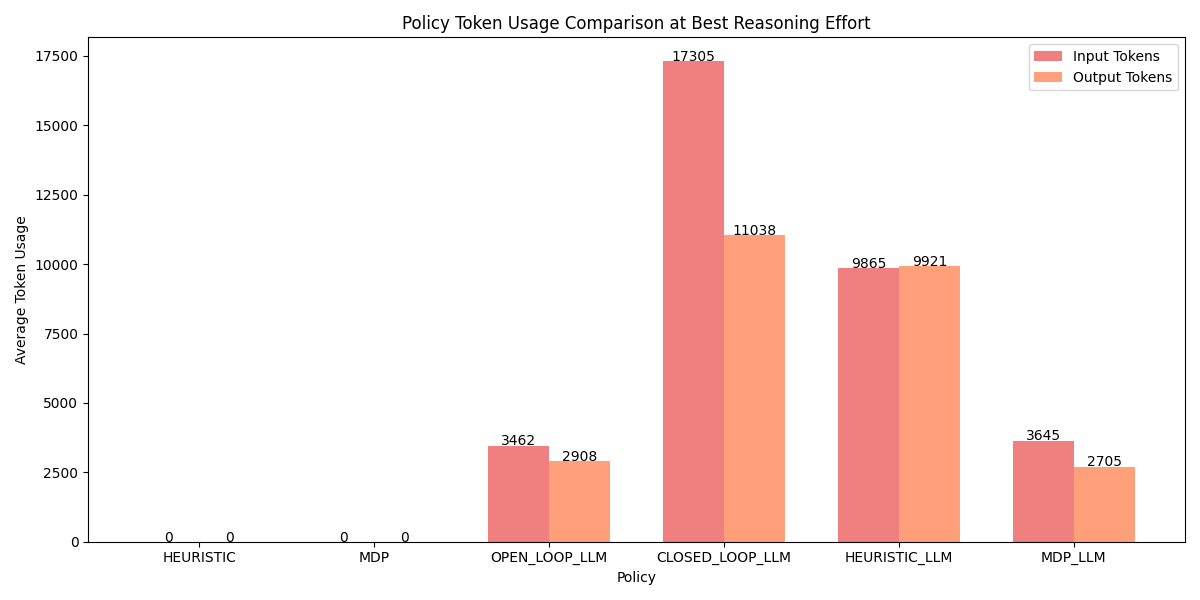
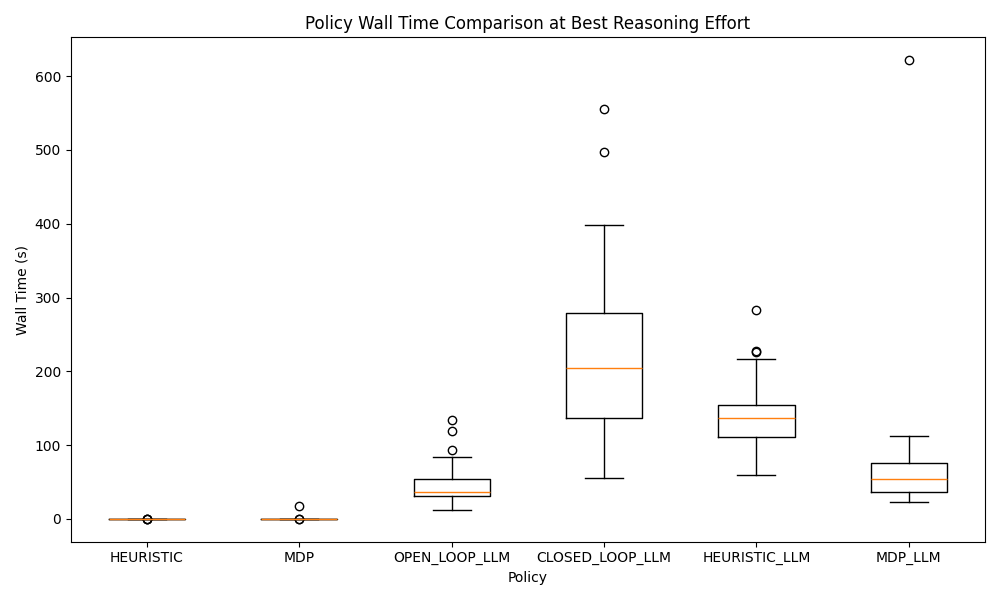
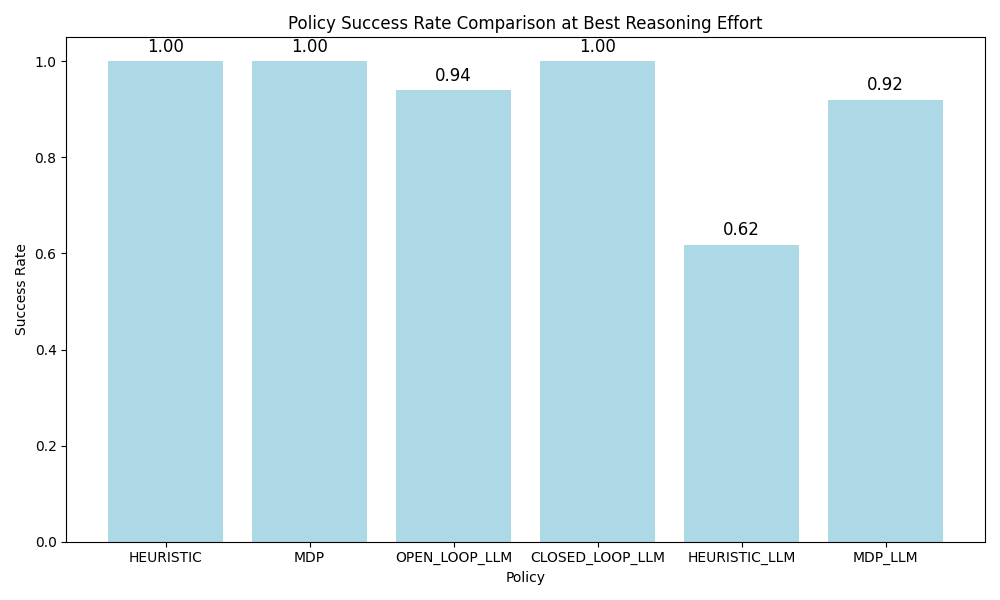
To wrap up the findings, I made some plots to compare the best performing reasoning level for each planner. While the medium level reasoning closed loop policy had a perfect track record, I found MDP-LLM to be the most practical for its high probability of producing an optimal policy. I was most surprised by two results:

• The stark difference in performance between the heuristic and MDP generation
• The consistently higher performance of medium reasoning over high reasoning

While I lack the tools to peer into GPT-5-mini's brain to figure out the second finding, the first finding likely follows that it's easier to "define" this problem (as an MDP) than it is to "solve" for it (by codifying some problem solving skills). A neat thought is that the tabular MDP model it created is more difficult to write down than a simple generative model, so the problem could be formulated to be even easier without adding complexity to the system prompt.

These findings also, in my opinion, answer two of those initial research questions. LLMs have a limit on the "make me smarter" knobs, and, situationally, LLMs can be amazingly practical at modeling a problem. While I did not compare detailed prompts to hand-hold the LLM through each problem, there was still reasonable success in giving minimal, straightforward prompts and letting the LLM "think" for itself.